目录

1、基本介绍
过拟合:指为了得到一致性假设而使假设变得过度严格。在模型参数拟合过程中,由于训练数据包含抽样误差,复杂的模型将抽样误差也考虑在内,将抽样误差也进行了很好的拟合。
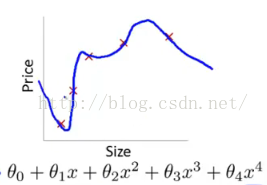
当训练数据不够多时,者over-training时,经常会导致over-fitting(过拟合),如下图所示:
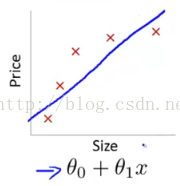
- 欠拟合:指模型没有很好地捕捉到数据特征,不能很好地拟合数据。
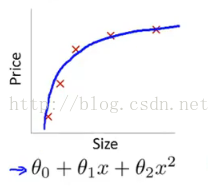
如上左图,由于是一次函数,没有很好的拟合数据;右图是二次函数,能够较好地拟合所有数据。究其原因,两者之间的差别在于有没有二次项系数,即参数多少的问题。
2、原因
过拟合的根本原因:特征维度过多,模型假设过于复杂,参数过多,训练数据过少,噪声过多,导致拟合的函数完美的预测训练集,但对新数据的测试集预测结果差。 过度的拟合了训练数据,而没有考虑到泛化能力。因此需要减少特征维度,或者正则化降低参数值。
欠拟合的根本原因:特征维度过少,模型过于简单,导致拟合的函数无法满足训练集,误差较大; 因此需要增加特征维度,增加训练数据。
3、解决方法
避免过拟合的方法:
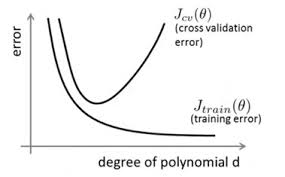
交叉验证:即重复使用数据,把得到的样本数据进行切分,组合为不同的训练集和测试集,用训练集训练模型,用测试集来评估模型预测的好坏。由于在此基础上可以得到多组不同的训练集和测试集,某次训练集中的某样本在下次可能成为测试集中的样本,即所谓“交叉”。当数据量不是很充足的时候,会使用交叉验证。
在训练过程中,我们通经常使用它来确定一些超參数(比方,依据validation data上的accuracy来确定early stopping的epoch大小、依据validation data确定learning rate等等。
正则化:(L1和L2)通过改动代价函数实现。
数据增强:增加训练数据样本。
Dropout:通过改动神经网络本身来实现。例如,训练前,随机删除一部分隐层单元,保持输入输出层不变,依照BP算法更新上图神经网络中的权值。
early stopping:即提前终止。Early stopping是一种以迭代次数截断的方法来防止过拟合。
Bagging用不同的模型拟合不同部分的训练集;Boosting只使用简单的神经网络;
数据清洗:将错误的label纠正或者删除错误的数据。
为什么说数据量大了以后,求解\(min Cost\)函数时候,模型为了求解到最小值过程中,需要兼顾真实数据拟合和随机误差拟合,所有样本的真实分布是相同的(都是猴子),而随机误差会在一定程度上抵消(猴子的肤色——黄色)。——训练数据中全是黄色猴子,测试数据中一旦是白色猴子就检测不出来。
欠拟合的解决方法:
添加其他特征项:添加特征的重要手段是“组合”,“泛化”,“相关性”;另外,特征添加的首选项是“上下文特征”,“平台特征”。
添加多项式特征:比较常用,例如,在线性模型中通过添加二次项或者三次项使模型的泛化能力更强。
减少正则化参数:特征化的目的是用来防止过拟合的。
4、正则化
正则化是模型选择的典型方法,是结构风险最小化策略的实现。一般是在经验风险上加上一个正则化项或罚项,正则化一般是模型复杂度的单调递增函数,模型越复杂,正则化值就越大。
正则化项的函数形式为:
\[min_{f \in F} \quad \frac{1}{N} \sum_{i=1}^{N} L(y_{i}, f_{x_{i}}) + \lambda J(f)\]
其中第一项是经验风险,第二项是正则化项,\(\lambda>0\)为调整两者之间关系的系数。
正则化项\(\lambda J(f)\)可以取不同的形式。回归问题中,损失函数\(L(y_{i}, f_{x_{i}}\)是平方损失,正则化项是参数向量的\(L_{2}\)范数。
正则化的优点是:
能保留所有的特征,但是降低参数\(\omega_{j}\)的量/值。
正则化的好处是但特征很多时,每一个特征都会对预测\(f(x_{i})\)贡献一份合适的力量。
4.2 L2正则化
- L2正则化是指正则化项为参数向量的\(L_{2}\)范数。相应的经验风险(损失函数)为:
\[L(\omega) = \frac{1}{N} \sum_{i=1}^{N} (f(x_{i}) - y_{i})^{2} + \frac{\lambda}{2} ||\omega||^{2}\]
- 2-范数:\(||x||_{2} = \sqrt {\sum_{i=1}^{N} |x_{i}|^{2}}\),欧几里得范数,即向量元素绝对值的平方和再开方。常用于计算向量长度。
理解L2、L1正则化可参考4
4.1 L1正则化
- L1正则化是指正则化项为参数向量的\(L_{1}\)范数。相应的经验风险(损失函数)为:
\[L(\omega) = \frac{1}{N} \sum_{i=1}^{N} (f(x_{i}) - y_{i})^{2} + \frac{\lambda}{2} ||\omega||^{1}\]
- 1-范数:\(||x||_{1} = \sum_{i=1}^{N} |x_{i}|\),即元素绝对值之和。
参考:
李航《统计学习方法》
正则化原理通俗理解:
建议参考: